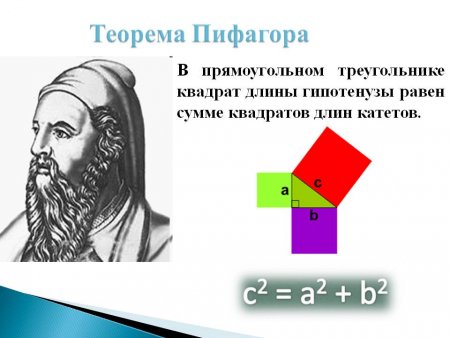
Тренажер можно использовать как для обучающихся 9 класса в качестве подготовки к экзамену, так и для обучающихся 8 класса для отработки умения пользоваться теоремой Пифагора в жизненных ситуациях.

Ресурс может быть включен в урок на любом его этапе: повторения, закрепления изученного, актуализации опорных знаний и др. 

   Устный счет в математике является инструментом для актуализации имеющихся у обучающихся знаний, что позволяет эффективно организовать дальнейшее изучение темы.
  Устный счет может быть включен в учебное занятие с целью обобщения, закрепления или коррекции знаний обучающихся.
  При регулярном использовании устного счета уровень вычислительных навыков может быть доведен до автоматизма, что значительно облегчает работу над многими темами программы. 

В данном тесте проверяются теоретические знания по геометрии. В каждом вопросе несколько вариантов ответа.


При нажатии на неправильный ответ, дается дополнительная информация объясняющая почему данное решение ученика неверно. Разъясняются основные понятия, и наглядно изображается правильный вариант ответа.

Вторым заданием в ЕГЭ по математике профильного уровня, является работа с графиком или диаграммой.
 
Основная задача в этих заданиях проверить навыки работы с графическими изображениями, получением данных и на их основании правильно определить ответ.

Давайте рассмотрим два задания стандартного типа, в которых используются графики и диаграммы:

   Для начала, давайте рассмотрим основные типы задач, которые могут нам встретиться в третьем задании ЕГЭ по профильной математике.

Их можно разделить на следующие группы:

• Многоугольники: вычисление длин и углов.
• Многоугольники: вычисление площади.
• Круг и его элементы.
• Координатная плоскость.

В этой статье мы постараемся  ответить на часто задаваемый вопрос: -« Как решать задания на определение вероятности?».
 
Задачи такого типа мы встречаем в 4 задании ЕГЭ по математике профильного уровня.

Сама тема « Нахождение вероятности» не является сложной в вычислительной части, трудности возникают в определении способа решения данного типа задач.

80% задач на определение вероятности решаются по формуле Р(А) = число благоприятных событий/ общее число событий, где Р(А) – искомая вероятность событий.

Производная в графике функции и график производной функции — это одно понятие?

 Или речь идет о разных структурах?

В чем же различие между производной в графике функции и графиком производной функции?

Общая информация

Цели: расширить общий кругозор учащихся; повысить информационную грамотность; распространить правила безопасности в сети; вызвать интерес к предмету; заинтересовать в углубленном изучении информатики и ИКТ-технологий.

Задачи: развивать универсальные учебные действия учащихся: внедрить и отработать навыки работы с технологиями ТРКМ и ТРИЗ; создать ряд проектов в рамках реализации проектной деятельности учащихся; выявить и продолжить работу с одаренными детьми; дать возможность учащимся проявить себя, тем самым научить работать в группе, самостоятельно.

  Впервые знакомясь со свойствами парных углов, учащиеся не сразу их запоминают. Им кажется, что это легкая тема, ведь здесь не нужно учить формулы, запоминать определения. А зря! 

   Зачатую, от применения свойств углов, зависит правильное решение геометрических задач. Исходя из данных в условии задач, свойства углов могут:

1. Приводить к конечному результату или содержать его;
2. Сделать промежуточный вывод, приводимый к следующему этапу решения.

   Учебный проект -учебно-познавательная, творческая или игровая деятельность учащихся, имеющая общую цель и согласованные способы, направленные на достижение общего результата  по решению какой-либо проблемы, значимой для участников проекта.

   Возможными источниками проблемы могут выступать противоречия:

• между известным и  неизвестным
• между знаниями  и умениями
• между сложностью задачи и наличием способа ее решения
• между потребностями и возможностями их реализации
• между житейскими представлениями и научными знаниями