Применение свойств углов при решении геометрических задач.
Впервые знакомясь со свойствами парных углов, учащиеся не сразу их запоминают. Им кажется, что это легкая тема, ведь здесь не нужно учить формулы, запоминать определения. А зря! Зачатую, от применения свойств углов, зависит правильное решение геометрических задач. Исходя из данных в условии задач, свойства углов могут:
- Приводить к конечному результату или содержать его;
- Позволять сделать промежуточный вывод, приводимый к следующему этапу решения.
Незнание названий и свойств углов отрицательно сказывается на качестве понимания и решения геометрических задач. Не поняв, упустив «малое»-невозможно решать более сложные формы заданий по геометрии. Нет легких или не важных тем! Все темы взаимосвязаны друг с другом, главное знать, понимать и применять эту связь при работе над заданием.
В этой статье, мы:
А) Познакомимся с названиями углов;
Б) Рассмотрим свойства каждой пары;
В) Изучим применение этих свойств на конкретных примерах геометрических задач;
Г) Сравним несколько способов решения.
Названия углов
Различают:
-Односторонние;
-Вертикальные;
-Соответственные;
-Смежные;
-Накрест лежащие углы.
- Вертикальные углы. В их названиях отражается расположение пара углов между собой. Например, смежные углы — это пара углов, у которых одна сторона общая, т.е. они расположены через стенку.
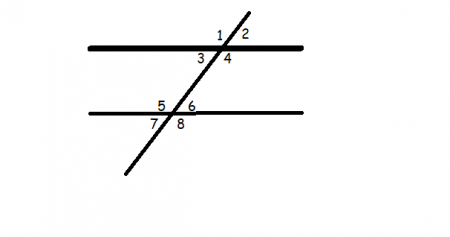
Для наглядного объяснения используем простейшее геометрическое построение. Выпишем обозначения углов.
| Вертикальные: 1 и 4 6 и 7 …. Смежные: 1 и 2 6 и 8 ……. Соответственные: 1 и 5 4 и 8... Накрест лежащие: 3 и 6 4 и 5 Односторонние: 3 и 5 4 и 6 |
Каждая пара этих углов имеет определенные свойства. Знание и применение этих свойств помогут вам при решении геометрических задач.
Свойства углов.
Разделяют всего два свойства углов:
- Сумма углов равна 180°.
- Углы между собой равны.
Составим опорную таблицу. Она позволит наглядно увидеть какие свойства у каждой пары углов.
Свойства | Сумма углов равна 180°. | Углы между собой равны |
Название углов | Смежные Односторонние | Вертикальные Соответственные Накрест лежащие |
Попробуем закрепить наш материал на практике.
Решение геометрических задач
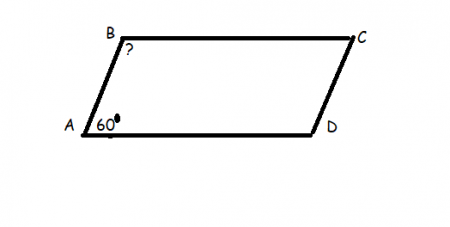
Задача 1
Условие: Дан параллелограмм АВСD Угол (∟А) равен 60°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
| Решение. 1)У параллелограмма два угла –острых, два тупых (свойства параллелограмма). При этом они между собой равны. ∟А=∟С (60°) угол меньше 90°-острый, тогда ∟В=D∟-? (нужно найти) 2)Заметим, что ∟А с ∟В составляют пару односторонних углов. А значит их сумма должна равняться 180 °. 3) Вычислим: ∟А+∟В = 180° 60°+∟В= 180° ∟В= 180°-60° ∟В=120° Ответ: 120° | Графическое построение (чертеж)
|
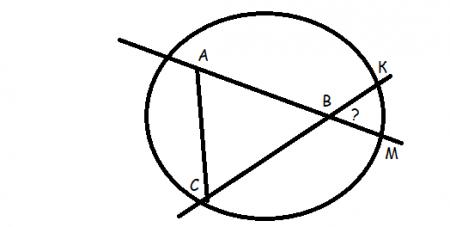
Задача 2
Условие В окружности найдите угол КВМ между секущими АМ и СК зная, что треугольник АВС – равносторонний. Ответ дайте в градусах. | Решение Как видим в данной задачи нет никаких числовых данных. Все ее решение основано на знаниях свойств, определений и умении выстраивания логических связей. 1.Треугольник АВС- равносторонний по условию А это значит у него все стороны и углы равны между собой. (св-со равностороннего треугольника); также мы знаем, что сумма углов любого треугольника равна 180˚. Следовательно: Х+Х+Х=180 3Х=180 Х= 60 2. Угол КВМ (внешний)и угол АВС- вертикальные, а значит они равны между собой. В конечном результате получается, что угол КВМ =60˚
| Графическое построение (чертеж)
|
Заключение
Как Вы убедились, опираясь на свойства углов, процесс решения задач несложный и понятный. Одну и ту же задачу можно решить разными способами. Все зависит как от условия задачи, так и от той логической связи, на которую вы будете опираться в процессе решения. Как всегда, повторюсь, что сложное – это несколько простых и понятных шагов!
Не спешите! Поэтапно, шаг за шагом выстраивайте логическую цепочку решения. Если не получается – отступите на пару шагов. Подумайте, посмотрите на решение под другим углом, постройте другую линию рассуждений.
Отступление –это не проигрыш, это стратегия выигрыша, которая позволяет более тщательнее подготовиться к успешной атаке!
В результате, самая сложная задача будет Вами решена! Успехов