Таблица значений тригонометрических функций. Быстро и легко!

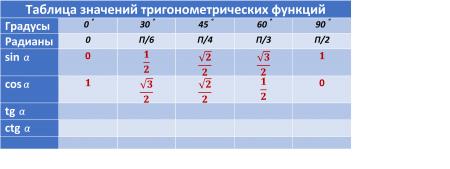Особый страх учеников вызывает таблица значений тригонометрических функций.
С чем это связанно? На взгляд учащихся, значения функций расставлены бессистемно и хаотично. При этом, значения могут быть отрицательными. Содержать дроби и корни. А где-то ответ вообще отсутствует. В совокупности, эти причины приводят учеников к мысли, что это невозможно запомнить. При этом, заученные значения легко перепутать.

Все эти страхи беспочвенны!
    Как я уже говорила ранее, любое сложное-это цепочка более простых, логических действий. Конечно, в математике, как и в других науках, необходимо учить формулы, определения, следствия и т. д. Но понимание смысла изучаемого, принесет больше пользы, чем бездумное заучивание. Понять принцип, изучить процесс действий позволит в дальнейшем проводить причино – следственные связи, находить логическую основу темы. В результате, самая сложная и «страшная» тема -станет простой и легкой. А это значит, таблица значений тригонометрических функций не так страшна, как кажется.

Постепенно все, что казалось сложным, становится простым.
Пауло Коэльо. Книга воина света

Итак, начнем….
     Очень внимательно рассмотрим расстановку значений в таблице. Что же мы видим? Определенно прослеживается некая закономерность в значениях. Попробуем понять ее.
     Наша основная цель: научиться самим составлять и заполнять таблицу значений тригонометрических функций.
Для этого нам понадобиться:

• — маленькие «хитрости» (лайфхаки);
• -знание свойств тригонометрических функций;
• — знание знаков каждой функции.

Лайфхак – это успешно функционирующий способ (решение), чтобы быстро и без особых усилий совершить какое-то действие.

Расстановка градусных и радианных мер в таблице значений тригонометрических функций.

   В таблице используются градусные и радианные меры измерения углов. Обычно ученики хорошо запоминают градусные меры. В тоже время, хочется напомнить «ассоциационный» метод, который поможет не ошибиться.

Первый лайфхак.

Определение угла. Используется «ассоциационный» метод —«рука».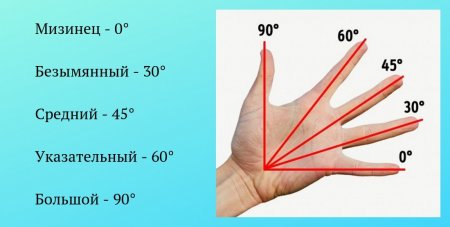

Этот простой и удобный способ поможет Вам в разных ситуациях.  В данном случае, он позволит Вам правильно записать градусные и радианные меры угла.

Лайфхак второй

1. В строчку значений синусов запишем числа-0,1,2,3,4;
2. Используем формулу для каждого значения;
3. Вычислим результат.

Рассмотрим процесс вычисления по формуле:

Вставим полученные результаты в таблицу:

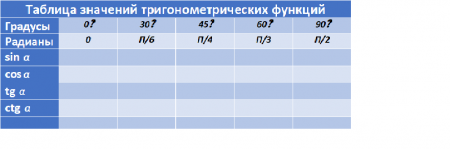
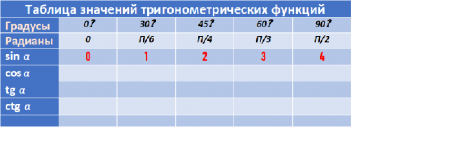
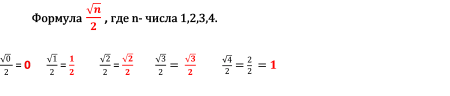
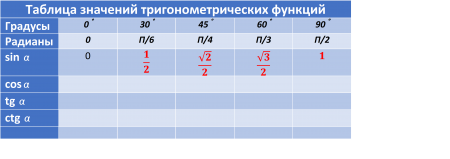
Лайфхак третий.

Запишем значения косинуса «зеркально» (наоборот). С конца в начало. Тем самым у нас получиться:

Наши маленькие «хитрости» позволили найти значения синуса и косинуса. Тем самым мы получили основу, которая поможет заполнить оставшуюся часть таблицы.
 А для этого мы вспомним …….

Свойства тригонометрических функций.

Известно, что:

• -тангенсом угла называется отношение противолежащего катета к прилежащему;
• или еще говорят, что, тангенс угла равен отношению синуса к косинусу данного угла.

Ориентируясь на второе определение, мы получим значения тангенса и внесем их в таблицу.

Внесем полученные значения в таблицу. При этом, таблица значений тригонометрических функций приобретает следующий вид:

Осталось занести значения котангенса. Это можно сделать двумя способами.
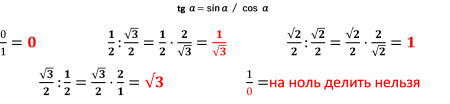
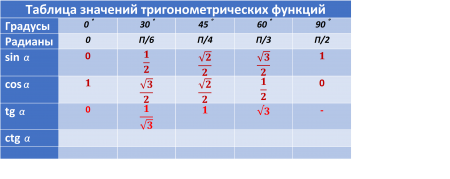
Первый способ ориентирован на свойства котангенса.
Котангенс угла равен отношению косинуса к синусу данного угла.

Используя это отношение, как и в предыдущем случае, вычисляем значения котангенса.
Второй способ основан на знакомом нам «зеркальном» лайфхаке.
Зная, что отношения котангенса — это обратное отношение тангенса, мы переписываем значения, наоборот. С конца в начало.

В нашей таблице мы рассмотрели значения функций на промежутке от 0 до 90 градусов. Данный угол соответствует первой четверти.
Попробуем продолжить нашу таблицу, расширив диапазон значений. Главное знать ……

Знаки тригонометрических функции.

В первой четверти — все тригонометрические функции положительны.
Во второй четверти:

• Синус имеет знак «плюс»-его значения будут положительными;
• Косинус, тангенс, котангенс содержат знак «минус»- их значения станут отрицательными.

Как видим, мы расставили градусные и радианные меры в таблице. Осталось внести значения.
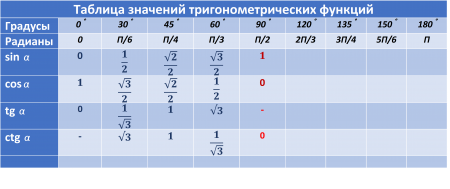
Есть два способа, не сильно отличающиеся друг от друга. И для одного и другого, опорной точкой служит столбик 90˚. Для обоих способов – это своеобразная «граница». Изучим их более подробно.

1. «Зеркальный»-построчное заполнение зеркально отраженных значений. (Условное зеркало – столбик 90˚).

2.«Осевой»-основан на принципах осевой симметрии. (Условная ось– столбец 90˚).

Как Вы наглядно увидели, существенных различий у двух способов нет. И в том и другом способе мы получим:

В результате, перед нами таблица значений тригонометрических функций от 0˚ до 180˚.
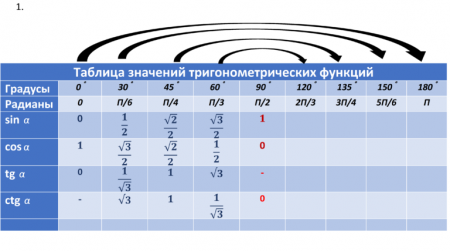
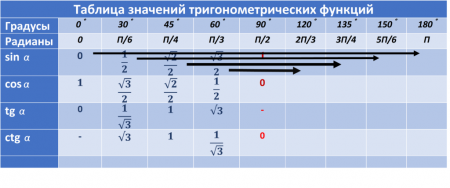
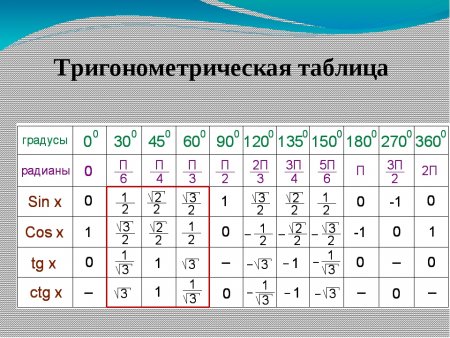
При этом нам не понадобилось её заучивать!
Надеюсь, эта статья будет Вам полезна. А следовательно, поможет в решении заданий по тригонометрии.